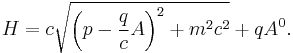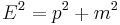Dirac equation
| Quantum field theory |
|---|
| History of... |
|
Equations
|
|
Incomplete theories
|
|
Scientists
Adler • Bethe • Bogoliubov • Callan • Candlin • Coleman • DeWitt • Dirac • Dyson • Fermi • Feynman • Fierz • Fröhlich • Gell-Mann • Goldstone • Gross • 't Hooft • Jackiw • Klein • Landau • Lee • Lehmann • Majorana • Nambu • Parisi • Polyakov • Salam • Schwinger • Skyrme • Stueckelberg • Symanzik • Tomonaga • Veltman • Weinberg • Weisskopf • Wilson • Witten • Yang • Yukawa • Hoodbhoy • Zimmermann • Zinn-Justin
|
In physics, more specifically relativistic quantum mechanics, the Dirac equation is a wave equation, formulated by British physicist Paul Dirac in 1928. It provided a description of elementary spin-½ particles, such as electrons, consistent with both the principles of quantum mechanics and the theory of special relativity, and was the first theory fully to account for relativity in the context of quantum mechanics. It accounted for the fine details of the hydrogen spectrum in a completely rigorous way. The equation also implied the existence of a new form of matter, antimatter, hitherto unsuspected and unobserved, and actually predated its experimental discovery. It also provided a theoretical justification for the introduction of several-component wave functions in Pauli's phenomenological theory of spin. Although Dirac did not at first fully appreciate what his own equation was telling him, his resolute faith in the logic of mathematics as a means to physical reasoning, his explanation of spin as a consequence of the union of quantum mechanics and relativity, and the eventual discovery of the positron, represents one of the great triumphs of theoretical physics, fully on a par with the work of Newton, Maxwell, and Einstein before him.
The Dirac equation
The equation in the form originally proposed by Dirac is: [1] [2]
where ψ = ψ(r, t) is the wave function for the electron, r and t are the space and time coordinates, m is the rest mass of the electron, 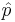 is the momentum operator, c is the speed of light, and ħ is the reduced Planck constant (h/2π).
is the momentum operator, c is the speed of light, and ħ is the reduced Planck constant (h/2π).
The dimension of each side of the equation is energy, recalling that cp (velocity × momentum), mc2 (rest energy), and ħ/t (action/time) are all energies. In light of this - there are some parallels with this equation and the Schrödinger equation. Both the same structure:
where the Schrödinger Hamiltonian is (sum of kinetic and potential energy):
and the Dirac Hamiltonian (sum of rest energy and energy due to momentum) is: [3]
In each case, the Hamiltonian is identified as the total energy of the particle:
-
total energy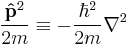
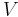
kinetic energy potential energy 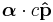
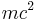
energy due to
momentumrest energy
The new elements in the Dirac equation, which do not occur in the Schrödinger equation, are the vector α = (α1, α2, α3), whose components are 4 × 4 matrices, β which is another 4 × 4 matrix, and the four-component wavefunction ψ. Hence the Dirac equation is actually a matrix equation - while the Schrödinger equation is simply a scalar equation. See below for its development and the mathematical details of the equation and matrices.
Dirac's purpose in casting this equation was to explain the behavior of the relativistically moving electron, and so to allow the atom to be treated in a manner consistent with relativity. His rather modest hope was that the corrections introduced this way might have bearing on the problem of atomic spectra. Up until that time, attempts to make the old quantum theory of the atom compatible with the theory of relativity, attempts based on discretizing the angular momentum stored in the electron's possibly non-circular orbit of the atomic nucleus, had failed - and the new quantum mechanics of Heisenberg, Pauli, Jordan, Schrödinger, and Dirac himself had not developed sufficiently to treat this problem. Although Dirac's original intentions were satisfied, his equation had far deeper implications for the structure of matter, and introduced new mathematical classes of objects that are now essential elements of fundamental physics.
The single symbolic equation thus unravels into four coupled linear first-order partial differential equations for the four quantities that make up the wave function. These matrices, and the form of the wave function, have a deep mathematical significance. The algebraic structure represented by the Dirac matrices had been created some 50 years earlier by the English mathematician W. K. Clifford. In turn, Clifford's ideas had emerged from the mid-19th century work of the German mathematician Hermann Grassmann in his "Lineale Ausdehnungslehre" (Theory of Linear Extensions). The latter had been regarded as well-nigh incomprehensible by most of his contemporaries. The appearance of something so seemingly abstract, at such a late date, and in such a direct physical manner, is one of the most remarkable chapters in the history of physics.
Mathematical formulation
Making the Schrödinger equation relativistic
The Dirac equation is superficially similar to the Schrödinger equation for a massive free particle:
The left side represents the square of the momentum operator divided by twice the mass m, which is the non-relativistic kinetic energy. Relativity treats space and time as a unified spacetime, a relativistic generalization of this equation requires that space and time derivatives must enter symmetrically, as they do in the Maxwell equations that govern the behavior of light — the equations must be differentially of the same order in space and time. In relativity, the momentum and the energy are the space and time parts of a space-time vector, the 4-momentum, and they are related by the relativistically invariant relation
which says that the length of this vector is proportional to the invariant mass m. Substituting the operator equivalents of the energy and momentum from the Schrödinger theory, we get an equation describing the propagation of waves, constructed from relativistically invariant objects, the Klein-Gordon equation:
where the wave function ψ is a relativistic scalar: a complex number which has the same numerical value in all frames of reference. The space and time derivatives both enter to second order. This has a telling consequence for the interpretation of the equation. Because the equation is second order in the time derivative, then by the nature of solving differential equations, one must specify both the initial values of the wave function itself and of its first time derivative, in order to solve definite problems. Because both may be specified more or less arbitrarily, the wave function cannot maintain its former role of determining the probability density of finding the electron in a given state of motion. In the Schrödinger theory, the probability density is given by the positive definite expression
and this density is convected according to the probability current vector
in terms of cartesian components:
The Schrödinger equation can be used to derive the continuity equation - a statement of the conservation of probability:
The fact that the density is positive definite and convected according to this continuity equation, implies that we may integrate the density over a certain domain and set the total to 1, and this condition will be maintained by the conservation law. A proper relativistic theory with a probability density current must also share this feature. Now, if we wish to maintain the notion of a convected density, then we must generalize the Schrödinger expression of the density and current so that the space and time derivatives again enter symmetrically in relation to the scalar wave function. We are allowed to keep the Schrödinger expression for the current, but must replace by probability density by the symmetrically formed expression
which now becomes the 4th component of a space-time vector, and the entire 4-current density has the relativistically covariant expression
where (translating usual cartesian-subscript notation into vector indicies): [4]
and the partial derivatives are
where 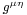 is the metric tensor. Using the (+−−−) metric signature and contracting on like indicies implies
is the metric tensor. Using the (+−−−) metric signature and contracting on like indicies implies  for
for  (the probability density component), and
(the probability density component), and  for
for 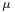 = 1, 2, 3 (the probability current components). Setting the index
= 1, 2, 3 (the probability current components). Setting the index 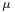 to these values returns the initial expressions for the current and density components. The continuity equation is as before:
to these values returns the initial expressions for the current and density components. The continuity equation is as before:
Everything is compatible with relativity now, but we see immediately that the expression for the density is no longer positive definite - the initial values of both ψ and 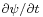 may be freely chosen, and the density may thus become negative, something that is impossible for a legitimate probability density. Thus we cannot get a simple generalization of the Schrödinger equation under the naive assumption that the wave function is a relativistic scalar, and the equation it satisfies, second order in time.
may be freely chosen, and the density may thus become negative, something that is impossible for a legitimate probability density. Thus we cannot get a simple generalization of the Schrödinger equation under the naive assumption that the wave function is a relativistic scalar, and the equation it satisfies, second order in time.
Although it is not a successful relativistic generalization of the Schrödinger equation, this equation is resurrected in the context of quantum field theory, and describes a spinless particle field (e.g. pi meson). Historically, Schrödinger himself arrived at this equation before the one that bears his name, but soon discarded it. In the context of quantum field theory, the indefinite density is understood to correspond to the charge density, which can be positive or negative, and not the probability density.
Dirac's deduction of the equation
Dirac thus thought to try an equation that was first order in both space and time. One could, for example, formally take the relativistic expression for the energy
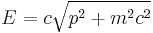 ,
,
replace p by its operator equivalent, expand the square root in an infinite series of derivative operators, set up an eigenvalue problem, then solve the equation formally by iterations. Most physicists had little faith in such a process, even if it were technically possible.
As the story goes, Dirac was staring into the fireplace at Cambridge, pondering this problem, when he hit upon the idea of taking the square root of the wave operator thus:
On multiplying out the right side, it can be noticed that the cross-terms, such as 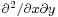 , will vanish if we assume that for every different pair of matrices their anticommutator vanishes:
, will vanish if we assume that for every different pair of matrices their anticommutator vanishes:
and that they each square to the 4 × 4 identity:
Dirac, who had just then been intensely involved with working out the foundations of Heisenberg's matrix mechanics, immediately understood that these conditions could be met if A, B, C and D are matrices, with the implication that the wave function has multiple components. This immediately explained the appearance of two-component wave functions in Pauli's phenomenological theory of spin, something that up until then had been regarded as mysterious, even to Pauli himself. However, one needs at least 4 × 4 matrices to set up a system with the properties required — so the wave function had four components, not two, as in the Pauli theory, or one, as in the bare Schrödinger theory. The four-component wave function represents a new class of mathematical object in physical theories, spinors, that makes its first appearance here.
Given the factorization in terms of these matrices, one can now write down immediately an equation
with X to be determined. Applying again the matrix operator on both side yields
On setting
we find that all the components of the wave function individually satisfy the relativistic energy–momentum relation. Thus the sought-for equation that is first-order in both space and time is
Setting
substituting and factoring iβ, inserting the gradient operator ∇, then multiplying both sides by ħc and expanding:
since
multiplying both sides by β:
finally inserting the momentum operator
yeilds the Dirac equation as above
Some different forms of the equation are outlined below, and the nature of the matrices are summarized.
The Dirac α and β matrices
Starting from the the original form Dirac equation:
The matrices α1, α2, α3, and β, are 4 × 4 matrices. Some properties are as follows:
They are all Hermitian so that the Dirac Hamiltonian is Hermitian.
They have squares equal to the 4 × 4 identity matrix I4:
and they all mutually anticommute:
for all i not equal to j. The brackets [ , ]+ denote the anticommutator:
Dirac defined these matrices as the following: [5]
NB: In the literature and this context, all matrices are usually written in italic like scalars, bold is used for a vector whose components are matrces. Superscript and subscript indicies are used to label components of the vectors of matrices. See Covariance and contravariance of vectors - except for identity matrices. Also it is conventional not to write identity matrices, or write them as 1, as they can be revealed from their positions in the equation. If a matrix is shown as 2 × 2 when it is known to be 4 × 4, then the missing identities are the 2 × 2 identity matrix, I2. If no matrix is shown at all in the full Dirac equation, then it is understood that the missing identity is 4 × 4 identity matrix, I4.
The Dirac γ matrices
It is useful to define new matrices: [6]
(superscripts are contravariant vector indices, not powers) so that
These matrices are known as the gamma matrices, and there are two representations of them: [7] the Pauli-Dirac representation (and basis):
or the chiral representation (and basis):
Using the chiral basis the Dirac equation becomes:
This is a particularly useful way to write the equation, since it can be immediately translated into the language of 4-vectors and relativistic covariance can be demonstrated (see below), while it resembles a similar form to the original.
The Pauli spin σ matrices
The Dirac matrices are block matrices; where the partitions are the 2 × 2 zero matrix, the 2 × 2 Identity matrix I2, and the Pauli matrices σx, σy, σz (equivalently written σ1, σ2, σ3). In practice these rather large matrices can be written in the following standard representations: the α and β matrices are
the Pauli-Dirac basis is
and the chiral basis is:
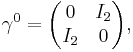
where  are as before.
are as before.
These can be written in terms of the Kronecker product (aka direct product, denoted by  or sometimes
or sometimes 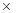 ) [8][9] of the matrices
) [8][9] of the matrices
and
where
is a vector whose components are the Pauli matrices.
The Dirac equation can then be written directly in terms of the Pauli σ matrices, illustrating how the Dirac theory accounts for Pauli's theory of spin. Substituting the α and β matrices leads to
Starting from
1. Direct substitution of the block matrices and the energy operator:
gives
collecting terms onto the left side
collecting everything into matrices
factor out the negative sign
yeilds
2. Direct substitution of the products of matrices (also inserting the energy operator) obtains:
collecting all terms into the matrices
factor out the negative sign
yeilds
Covariant form and relativistic invariance
To demonstrate the relativistic invariance of the equation, it is advantageous to cast it into a form in which the space and time derivatives appear on an equal footing. The equation takes the form:[10]
The complete system is summarized using the Minkowski metric on spacetime in the form
where again [ , ]+ denotes the anticommutator. These are the defining relations of a Clifford algebra over a pseudo-orthogonal 4-d space with metric signature 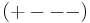 . The specific Clifford algebra employed in the Dirac equation is known today as the Dirac algebra. Although not recognized as such by Dirac at the time the equation was formulated, in hindsight the introduction of this geometric algebra represents an enormous stride forward in the development of quantum theory.
. The specific Clifford algebra employed in the Dirac equation is known today as the Dirac algebra. Although not recognized as such by Dirac at the time the equation was formulated, in hindsight the introduction of this geometric algebra represents an enormous stride forward in the development of quantum theory.
The Dirac equation may now be interpreted as an eigenvalue equation, where the rest mass is proportional to an eigenvalue of the 4-momentum operator, the proportion being the speed of light:
In practice, physicists often use units of measure such that ħ = c = 1, known as "natural units". The equation then takes the simple form
A fundamental theorem states that if two distinct sets of matrices are given that both satisfy the Clifford relations, then they are connected to each other by a similarity transformation:
If in addition the matrices are all unitary, as are the Dirac set, then S itself is unitary;
The transformation U is unique up to a multiplicative factor of absolute value 1. Let us now imagine a Lorentz transformation to have been performed on the space and time coordinates, and on the derivative operators, which form a covariant vector. For the operator 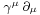 to remain invariant, the gammas must transform among themselves as a contravariant vector with respect to their spacetime index. These new gammas will themselves satisfy the Clifford relations, because of the orthogonality of the Lorentz transformation. By the fundamental theorem, we may replace the new set by the old set subject to a unitary transformation. In the new frame, remembering that the rest mass is a relativistic scalar, the Dirac equation will then take the form
to remain invariant, the gammas must transform among themselves as a contravariant vector with respect to their spacetime index. These new gammas will themselves satisfy the Clifford relations, because of the orthogonality of the Lorentz transformation. By the fundamental theorem, we may replace the new set by the old set subject to a unitary transformation. In the new frame, remembering that the rest mass is a relativistic scalar, the Dirac equation will then take the form
If we now define the transformed spinor
then we have the transformed Dirac equation in a way that demonstrates manifest relativistic invariance:
Thus, once we settle on any unitary representation of the gammas, it is final provided we transform the spinor according to the unitary transformation that corresponds to the given Lorentz transformation. The various representations of the Dirac matrices employed will bring into focus particular aspects of the physical content in the Dirac wave function (see below). The representation shown here is known as the standard representation - in it, the wave function's upper two components go over into Pauli's 2-spinor wave function in the limit of low energies and small velocities in comparison to light.
The considerations above reveal the origin of the gammas in geometry, harking back to Grassmann's original motivation - they represent a fixed basis of unit vectors in spacetime. Similarly, products of the gammas such as 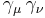 represent oriented surface elements, and so on. With this in mind, we can find the form of the unit volume element in spacetime in terms of the gammas as follows. By definition, it is
represent oriented surface elements, and so on. With this in mind, we can find the form of the unit volume element in spacetime in terms of the gammas as follows. By definition, it is
For this to be an invariant, the epsilon symbol must be a tensor, and so must contain a factor of 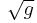 , where g is the determinant of the metric tensor. Since this is negative, that factor is imaginary. Thus
, where g is the determinant of the metric tensor. Since this is negative, that factor is imaginary. Thus
This matrix is given the special symbol 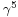 , owing to its importance when one is considering improper transformations of spacetime, that is, those that change the orientation of the basis vectors. In the standard representation it is
, owing to its importance when one is considering improper transformations of spacetime, that is, those that change the orientation of the basis vectors. In the standard representation it is
This matrix will also be found to anticommute with the other four Dirac matrices. It takes on a leading role when questions of parity arise, because the volume element as a directed magnitude changes sign under a space-time reflection. Taking the positive square root above thus amounts to choosing a handedness convention on space-time.
Adjoint equation and conservation of probability current
By defining the adjoint spinor
where 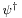 is the conjugate transpose of
is the conjugate transpose of 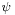 , and noticing that
, and noticing that
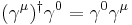 ,
,
we obtain, by taking the Hermitian conjugate of the Dirac equation and multiplying from the right by 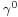 , the adjoint equation:
, the adjoint equation:
where 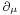 is understood to act to the left. Multiplying the Dirac equation by
is understood to act to the left. Multiplying the Dirac equation by 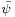 from the left, and the adjoint equation by
from the left, and the adjoint equation by  from the right, and subtracting, produces the law of conservation of the Dirac current:
from the right, and subtracting, produces the law of conservation of the Dirac current:
Now we see the great advantage of the first-order equation over the one Schrödinger had tried - this is the conserved current density required by relativistic invariance, only now its 4th component is positive definite and thus suitable for the role of a probability density:
Because the probability density now appears as the fourth component of a relativistic vector, and not a simple scalar as in the Schrödinger equation, it will be subject to the usual effects of the Lorentz transformations such as time dilation. Thus for example atomic processes that are observed as rates, will necessarily be adjusted in a way consistent with relativity, while those involving the measurement of energy and momentum, which themselves form a relativistic vector, will undergo parallel adjustment which preserves the relativistic covariance of the observed values.
Comparison with the Pauli theory
The necessity of introducing half-integral spin goes back experimentally to the results of the Stern–Gerlach experiment. A beam of atoms is run through a strong inhomogeneous magnetic field, which then splits into N parts depending on the intrinsic angular momentum of the atoms. It was found that for silver atoms, the beam was split in two—the ground state therefore could not be integral, because even if the intrinsic angular momentum of the atoms were as small as possible, 1, the beam would be split into 3 parts, corresponding to atoms with Lz = −1, 0, and +1. The conclusion is that silver atoms have net intrinsic angular momentum of 1⁄2. Pauli set up a theory which explained this splitting by introducing a two-component wave function and a corresponding correction term in the Hamiltonian, representing a semi-classical coupling of this wave function to an applied magnetic field, as so:
Here A and 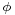 represent the electromagnetic field, and the three sigmas are the Pauli matrices. On squaring out the first term, a residual interaction with the magnetic field is found, along with the usual classical Hamiltonian of a charged particle interacting with an applied field:
represent the electromagnetic field, and the three sigmas are the Pauli matrices. On squaring out the first term, a residual interaction with the magnetic field is found, along with the usual classical Hamiltonian of a charged particle interacting with an applied field:
This Hamiltonian is now a 2 × 2 matrix, so the Schrödinger equation based on it must use a two-component wave function. Pauli had introduced the 2x2 sigma matrices as pure phenomenology— Dirac now had a theoretical argument that implied that spin was somehow the consequence of the marriage of quantum mechanics to relativity. On introducing the external electromagnetic 4-vector potential into the Dirac equation in a similar way, known as minimal coupling, it takes the form (in natural units)
A second application of the Dirac operator will now reproduce the Pauli term exactly as before, because the spatial Dirac matrices multiplied by i, have the same squaring and commutation properties as the Pauli matrices. What is more, the value of the gyromagnetic ratio of the electron, standing in front of Pauli's new term, is explained from first principles. This was a major achievement of the Dirac equation and gave physicists great faith in its overall correctness. There is more however. The Pauli theory may be seen as the low energy limit of the Dirac theory in the following manner. First the equation is written in the form of coupled equations for 2-spinors with the units restored:
so
Assuming the field is weak and the motion of the electron non-relativistic, we have the total energy of the electron approximately equal to its rest energy, and the momentum going over to the classical value,
and so the second equation may be written
which is of order v/c - thus at typical energies and velocities, the bottom components of the Dirac spinor in the standard representation are much suppressed in comparison to the top components. Substituting this expression into the first equation gives after some rearrangement
The operator on the left represents the particle energy reduced by its rest energy, which is just the classical energy, so we recover Pauli's theory if we identify his 2-spinor with the top components of the Dirac spinor in the non-relativistic approximation. A further approximation gives the Schrödinger equation as the limit of the Pauli theory. Thus the Schrödinger equation may be seen as the far non-relativistic approximation of the Dirac equation when one may neglect spin and work only at low energies and velocities. This also was a great triumph for the new equation, as it traced the mysterious i that appears in it, and the necessity of a complex wave function, back to the geometry of space-time through the Dirac algebra. It also highlights why the Schrödinger equation, although superficially in the form of a diffusion equation, actually represents the propagation of waves.
It should be strongly emphasized that this separation of the Dirac spinor into large and small components depends explicitly on a low-energy approximation. The entire Dirac spinor represents an irreducible whole, and the components we have just neglected to arrive at the Pauli theory will bring in new phenomena in the relativistic regime - antimatter and the idea of creation and annihilation of particles.
In a general case (if a certain linear function of electromagnetic field does not vanish identically), three out of four components of the spinor function in the Dirac equation can be algebraically eliminated, yielding an equivalent fourth-order partial differential equation for just one component. Furthermore, this remaining component can be made real by a gauge transform.[11]
Dirac equation in curved spacetime
The Dirac equation can be written in curved spacetime using vierbein fields. Vierbeins describe a local frame that enables to define Dirac matrices at every point. Contracting these matrices with vierbeins give the right transformation properties. This way Dirac's equation takes the following form in curved spacetime[12]:
Here 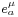 is the vierbein and
is the vierbein and 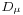 is the covariant derivative for fermion fields, defined as follows
is the covariant derivative for fermion fields, defined as follows
where 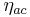 is the Lorentzian metric,
is the Lorentzian metric, 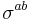 is the commutator of Dirac matrices:
is the commutator of Dirac matrices:
and 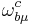 is the spin connection:
is the spin connection:
where 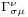 is the Christoffel symbol. Note that here, Latin letters denote the "Lorentzian" indices and Greek ones denote "Riemannian" indices.
is the Christoffel symbol. Note that here, Latin letters denote the "Lorentzian" indices and Greek ones denote "Riemannian" indices.
Physical interpretation
The Dirac theory, while providing a wealth of information that is accurately confirmed by experiments, nevertheless introduces a new physical paradigm that appears at first difficult to interpret and even paradoxical. Some of these issues of interpretation must be regarded as open questions. Here we will see how the Dirac theory brilliantly answered some of the outstanding issues in physics at the time it was put forward, while posing others that are still the subject of debate.
Identification of observables
The critical physical question in a quantum theory is - what are the physically observable quantities defined by the theory? According to general principles, such quantities are defined by Hermitian operators that act on the Hilbert space of possible states of a system. The eigenvalues of these operators are then the possible results of measuring the corresponding physical quantity. In the Schrödinger theory, the simplest such object is the overall Hamiltonian, which represents the total energy of the system. If we wish to maintain this interpretation on passing to the Dirac theory, we must take the Hamiltonian to be
This looks promising, because we see by inspection the rest energy of the particle and, in case A = 0, the energy of a charge placed in an electric potential qA0. What about the term involving the vector potential? In classical electrodynamics, the energy of a charge moving in an applied potential is
Thus the Dirac Hamiltonian is fundamentally distinguished from its classical counterpart, and we must take great care to correctly identify what is an observable in this theory. Much of the apparent paradoxical behavior implied by the Dirac equation amounts to a misidentification of these observables. Let us now describe one such effect. (continued)
Paradoxical behavior
The following problems arise with the Dirac equation, which are not immediately easy to interpret.
Klein paradox: when a Dirac electron interacts with an electric potential, the total probability is not conserved. Also, the electron can tunnel into high potential barriers, unlike the case in classical quantum mechanics described by the Schrödinger equation.
Zitterbewegung: apparent fluctuation (at the speed of light) of the position of an electron around the median.
Hole theory
The negative E solutions found in the preceding section are problematic, for it was assumed that the particle has a positive energy. Mathematically speaking, however, there seems to be no reason for us to reject the negative-energy solutions. Since they exist, we cannot simply ignore them, for once we include the interaction between the electron and the electromagnetic field, any electron placed in a positive-energy eigenstate would decay into negative-energy eigenstates of successively lower energy by emitting excess energy in the form of photons. Real electrons obviously do not behave in this way.
To cope with this problem, Dirac introduced the hypothesis, known as hole theory, that the vacuum is the many-body quantum state in which all the negative-energy electron eigenstates are occupied. This description of the vacuum as a "sea" of electrons is called the Dirac sea. Since the Pauli exclusion principle forbids electrons from occupying the same state, any additional electron would be forced to occupy a positive-energy eigenstate, and positive-energy electrons would be forbidden from decaying into negative-energy eigenstates.
Dirac further reasoned that if the negative-energy eigenstates are incompletely filled, each unoccupied eigenstate – called a hole – would behave like a positively charged particle. The hole possesses a positive energy, since energy is required to create a particle–hole pair from the vacuum. As noted above, Dirac initially thought that the hole might be the proton, but Hermann Weyl pointed out that the hole should behave as if it had the same mass as an electron, whereas the proton is over 1800 times heavier. The hole was eventually identified as the positron, experimentally discovered by Carl Anderson in 1932.
It is not entirely satisfactory to describe the "vacuum" using an infinite sea of negative-energy electrons. The infinitely negative contributions from the sea of negative-energy electrons has to be canceled by an infinite positive "bare" energy and the contribution to the charge density and current coming from the sea of negative-energy electrons is exactly canceled by an infinite positive "jellium" background so that the net electric charge density of the vacuum is zero. In quantum field theory, a Bogoliubov transformation on the creation and annihilation operators (turning an occupied negative-energy electron state into an unoccupied positive energy positron state and an unoccupied negative-energy electron state into an occupied positive energy positron state) allows us to bypass the Dirac sea formalism even though, formally, it is equivalent to it.
In certain applications of condensed matter physics, however, the underlying concepts of "hole theory" are valid. The sea of conduction electrons in an electrical conductor, called a Fermi sea, contains electrons with energies up to the chemical potential of the system. An unfilled state in the Fermi sea behaves like a positively-charged electron, though it is referred to as a "hole" rather than a "positron". The negative charge of the Fermi sea is balanced by the positively-charged ionic lattice of the material.
See also
- Bohr–Sommerfeld theory
- Breit equation
- Dirac field
- Einstein-Maxwell-Dirac equations
- Feynman checkerboard
- Foldy–Wouthuysen transformation
- Klein–Gordon equation
- Quantum electrodynamics
- Rarita–Schwinger equation
- Theoretical and experimental justification for the Schrödinger equation
- The Dirac Equation appears on the floor of Westminster Abbey. It appears on the plaque commemorating Paul Dirac's life which was inaugurated on November 13, 1995.[13]
References
- ^ Particle Physics (3rd Edition), B. R. Martin, G.Shaw, Manchester Physics Series, John Wiley & Sons, ISBN 978-0-470-03294-7
- ^ Quantum Field Theory, D. McMahon, Mc Graw Hill (USA), 2008, ISBN 978-0-07-154382-8
- ^ Quantum Field Theory, D. McMahon, Mc Graw Hill (USA), 2008, ISBN 978-0-07-154382-8
- ^ Quantum Field Theory, D. McMahon, Mc Graw Hill (USA), 2008, ISBN 978-0-07-154382-8
- ^ Quantum Mechanics, E. Abers, Pearson Ed., Addision Wesley, Prentice Hall Inc, 2004, ISBN 9780131461000
- ^ Quantum Field Theory, D. McMahon, Mc Graw Hill (USA), 2008, ISBN 978-0-07-154382-8
- ^ Quantum Field Theory, D. McMahon, Mc Graw Hill (USA), 2008, ISBN 978-0-07-154382-8
- ^ http://mathworld.wolfram.com/KroneckerProduct.html
- ^ Encyclopaedia of Physics (2nd Edition), R.G. Lerner, G.L. Trigg, VHC publishers, 1991, (Verlagsgesellschaft) 3-527-26954-1, (VHC Inc.) 0-89573-752-3
- ^ The Cambridge Handbook of Physics Formulas, G. Woan, Cambridge University Press, 2010, ISBN 978 0 521 57507 2
- ^ Source: Journal of Mathematical Physics, 52, 082303 (2011) (http://jmp.aip.org/resource/1/jmapaq/v52/i8/p082303_s1 or http://akhmeteli.org/wp-content/uploads/2011/08/JMAPAQ528082303_1.pdf )
- ^ Lawrie, Ian D.. A Unified Grand Tour of Theoretical Physics.
- ^ http://www.dirac.ch/PaulDirac.html
Selected papers
- P.A.M. Dirac "The Quantum Theory of the Electron", Proc. R. Soc. A (1928) vol. 117, no 778, 610-624
- P.A.M. Dirac "The Quantum Theory of the Electron", Proc. R. Soc. A117) link to the volume of the Proceedings of the Royal Society of London containing the article at page 610
- P.A.M. Dirac "A Theory of Electrons and Protons", Proc. R. Soc. A126) link to the volume of the Proceedings of the Royal Society of London containing the article at page 360
- C.D. Anderson, Phys. Rev. 43, 491 (1933)
- R. Frisch and O. Stern, Z. Phys. 85, 4 (1933)
Textbooks
- Halzen, Francis; Martin, Alan (1984). Quarks & Leptons: An Introductory Course in Modern Particle Physics. John Wiley & Sons. ISBN.
- Dirac, P.A.M., Principles of Quantum Mechanics, 4th edition (Clarendon, 1982)
- Shankar, R., Principles of Quantum Mechanics, 2nd edition (Plenum, 1994)
- Bjorken, J D & Drell, S, Relativistic Quantum mechanics
- Thaller, B., The Dirac Equation, Texts and Monographs in Physics (Springer, 1992)
- Schiff, L.I., Quantum Mechanics, 3rd edition (McGraw-Hill, 1968)
- Griffiths, D.J., Introduction to Elementary Particles, 2nd edition (Wiley-VCH, 2008) ISBN 978-3-527-40601-2.
External links
- The Dirac Equation at MathPages
- The Nature of the Dirac Equation, its solutions and Spin
- Dirac equation for a spin ½ particle
- Pedagogic Aids to Quantum Field Theory click on Chap. 4 for a step-by-small-step introduction to the Dirac equation, spinors, and relativistic spin/helicity operators.
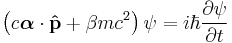
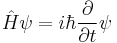
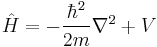
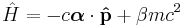
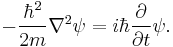
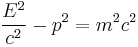
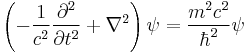
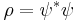
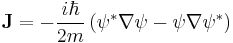
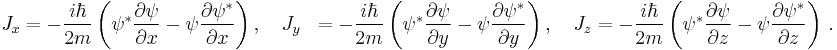
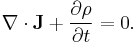
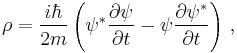
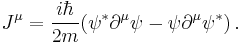
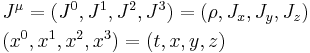
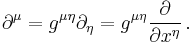
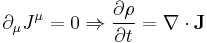
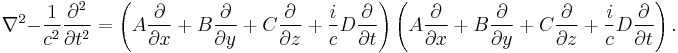
![[A,B]_%2B = 0, [A,C]_%2B = 0, \cdots \, ,](/2012-wikipedia_en_all_nopic_01_2012/I/89fe6cb86cf53b9f5c753803ac21bef4.png)
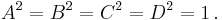
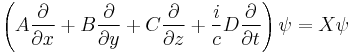
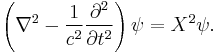
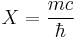
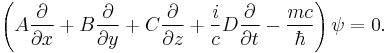
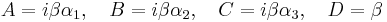
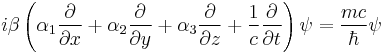
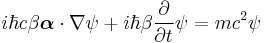
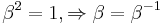
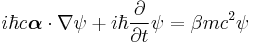
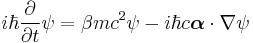
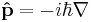
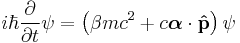
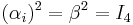
![[\alpha_i,\alpha_j]_%2B = 0 \,](/2012-wikipedia_en_all_nopic_01_2012/I/b456d01cdf2de95c5a5834f9356b5f6a.png)
![[\alpha_i,\beta]_%2B = 0 \,](/2012-wikipedia_en_all_nopic_01_2012/I/ed8ee081141d1f39a868f1abf4dd93e3.png)
![[A,B]_%2B = AB %2B BA \,](/2012-wikipedia_en_all_nopic_01_2012/I/f7ad33578fe04c0ddc8ba54b6198d92d.png)
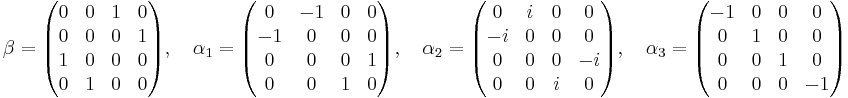
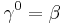
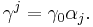
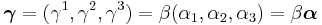
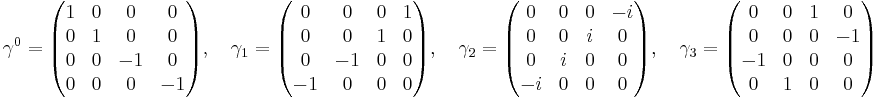
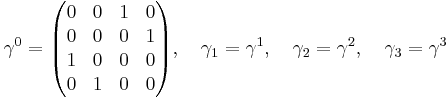
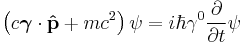
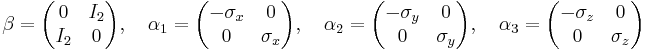
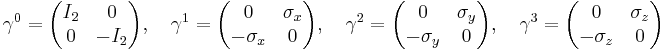
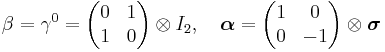
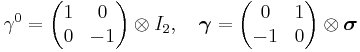
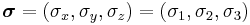
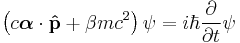
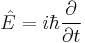
![\left[
c\begin{pmatrix}
\sigma_x & 0 \\
0 & -\sigma_x \\
\end{pmatrix}\hat{p}_x
%2Bc\begin{pmatrix}
\sigma_y & 0 \\
0 & -\sigma_y \\
\end{pmatrix}\hat{p}_y
%2Bc\begin{pmatrix}
\sigma_z & 0 \\
0 & -\sigma_z \\
\end{pmatrix}\hat{p}_z
%2B mc^2\begin{pmatrix}
0 & I_2 \\
I_2 & 0 \\
\end{pmatrix}
\right]\psi = I_4\hat{E}\psi](/2012-wikipedia_en_all_nopic_01_2012/I/7f74c26609e1f9f446a1f6b68ba93086.png)
![\left[
c\begin{pmatrix}
\sigma_x & 0 \\
0 & -\sigma_x \\
\end{pmatrix}\hat{p}_x
%2Bc\begin{pmatrix}
\sigma_y & 0 \\
0 & -\sigma_y \\
\end{pmatrix}\hat{p}_y
%2Bc\begin{pmatrix}
\sigma_z & 0 \\
0 & -\sigma_z \\
\end{pmatrix}\hat{p}_z
%2B mc^2\begin{pmatrix}
0 & I_2 \\
I_2 & 0 \\
\end{pmatrix}
- \begin{pmatrix}
I_2 & 0 \\
0 & I_2 \\
\end{pmatrix} \hat{E}
\right]\psi = 0](/2012-wikipedia_en_all_nopic_01_2012/I/a493c98763b3c9cd2938d227eba3cfbe.png)
![\left[ \begin{pmatrix}
-I_2 \hat{E} %2B c(\sigma_x\hat{p}_x%2B\sigma_y\hat{p}_y%2B\sigma_z\hat{p}_z) & 0 \\
0 & -I_2 \hat{E} -c(\sigma_x\hat{p}_x%2B\sigma_y\hat{p}_y%2B\sigma_z\hat{p}_z) \\
\end{pmatrix}
%2B mc^2\begin{pmatrix}
0 & I_2 \\
I_2 & 0 \\
\end{pmatrix}
\right]\psi = 0](/2012-wikipedia_en_all_nopic_01_2012/I/13647dca3537c991bf5968395c46c47d.png)
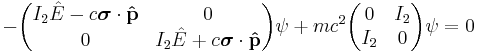
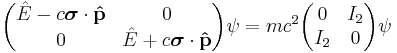
![\left[ c\begin{pmatrix}
1 & 0 \\
0 & -1 \\
\end{pmatrix}\otimes\boldsymbol{\sigma}\cdot\bold{\hat{p}}%2B \begin{pmatrix}
0 & 1 \\
1 & 0 \\
\end{pmatrix}\otimes I_2 mc^2\right]\psi = \hat{E}\psi](/2012-wikipedia_en_all_nopic_01_2012/I/7bb72401487f1ec212618f73ba265e3d.png)
![\left[ \begin{pmatrix}
c\boldsymbol{\sigma}\cdot\bold{\hat{p}} & 0 \\
0 & -c\boldsymbol{\sigma}\cdot\bold{\hat{p}} \\
\end{pmatrix} %2B \begin{pmatrix}
0 & I_2 mc^2 \\
I_2 mc^2 & 0 \\
\end{pmatrix} - I_4\hat{E} \right]\psi = 0](/2012-wikipedia_en_all_nopic_01_2012/I/cc8acd400232d7b14fa347357050bda2.png)
![\left[ \begin{pmatrix}
- \hat{E} %2B c\boldsymbol{\sigma}\cdot\bold{\hat{p}} & 0 \\
0 & - \hat{E} -c\boldsymbol{\sigma}\cdot\bold{\hat{p}} \\
\end{pmatrix} %2B \begin{pmatrix}
0 & I_2 mc^2 \\
I_2 mc^2 & 0 \\
\end{pmatrix} \right]\psi = 0](/2012-wikipedia_en_all_nopic_01_2012/I/384c660bf33da79ee1fce3ad1c4817af.png)
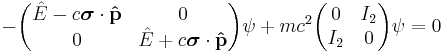
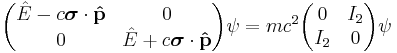
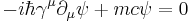
![[\gamma^\mu,\gamma^\nu ]_%2B = 2 g^{\mu\nu} \,](/2012-wikipedia_en_all_nopic_01_2012/I/4b28fd3b8889337069a4fddc546b1f39.png)
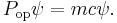
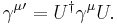
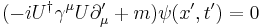
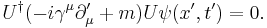
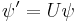
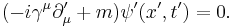
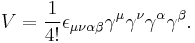
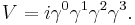
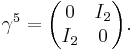
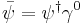
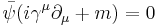
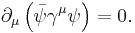
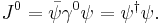
![H = \frac{1}{2m} \left [ \sigma\cdot \left ( p - \frac{e}{c}A \right ) \right ]^2 %2B e\phi.](/2012-wikipedia_en_all_nopic_01_2012/I/2adf2cba136d84381bc596e29712aa84.png)
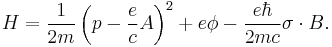
![\left [ -i\gamma^\mu\left ( \partial_\mu %2B ieA_\mu \right ) %2B m \right ] \psi = 0\,](/2012-wikipedia_en_all_nopic_01_2012/I/021121d51b43fa5fd356cd3ebf4b15ea.png)
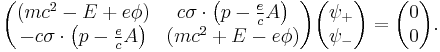
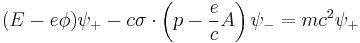
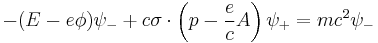
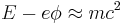
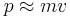
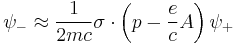
![( E - mc^2 ) \psi_%2B = \frac{1}{2m} \left [ \sigma\cdot \left ( p - \frac{e}{c}A \right ) \right ]^2 \psi_%2B %2B e\phi \psi_%2B](/2012-wikipedia_en_all_nopic_01_2012/I/8f93133461f87638b50ac034433bd4a5.png)
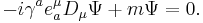
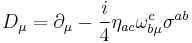
![\sigma^{ab}=\frac{i}{2} \left[\gamma^{a},\gamma^{b}\right]](/2012-wikipedia_en_all_nopic_01_2012/I/812d0e8c943b37ea6e2ffef732f5f54c.png)
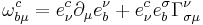
![H = \gamma^0 \left [ mc^2 %2B c \sum_{k = 1}^3 \gamma^k \left ( p_k-\frac{q}{c}A_k \right ) c \right ] %2B qA^0.](/2012-wikipedia_en_all_nopic_01_2012/I/71b97c013a4de3704d924320ec5a10d4.png)